
Surf forecasting isn’t just guesswork—it’s a combination of buoy data, math, and local knowledge that can help you make the call. Let’s walk through a real-world example where we compare two breaks on the same day and use some surf-nerdy calculations to pick the better option.
The Scene: Two Spots, One Swell#
It’s 6:00 AM. You’re sipping coffee in your van, torn between two nearby breaks: Main Beach, a wide-open stretch that usually delivers fun, cruisy waves, and Secret Ridge, a lesser-known spot up the coast rumored to fire when conditions align.
The buoy (our trusty Buoy 808) shows:
- Swell Height: 2.5 m
- Swell Period: 13 s
- Swell Direction: 225° (SW)
- Wind: Light offshore, 5 knots
Your surf app says both spots should be “Good,” but you know there’s more to it. Let’s use the numbers to figure out which break will be worth your paddle power.
Spot 1: Main Beach—The Crowd Pleaser#
Main Beach is a classic, user-friendly break. Its wide-open sandy bottom evenly spreads the incoming swell, making it great for long rides and mellow waves. However, sandy breaks like this don’t usually amplify swell energy—they tend to deliver waves as-is, straight from the buoy.
The Numbers for Main Beach#
Shoaling Factor: Why Waves Grow Taller Nearshore#
When waves travel from deep water into shallow water, they interact with the ocean floor, causing them to slow down, compress, and grow taller. This process is called shoaling, and the amount by which the wave height increases is described by the shoaling factor, written as:
$$ K_s = \sqrt{\frac{C_g}{C_{g,\text{shallow}}}} $$
Let’s break this down:
- \(K_s\): Shoaling factor, which tells us how much the wave height will increase.
- \(C_g\): Group velocity in deep water, or how fast wave energy moves far offshore.
- \(C_{g,\text{shallow}}\): Group velocity in shallow water, where the waves slow down as they approach the shore.
A \(K_s\) of 1.37 would mean the wave height grows by 37%.
What Is Group Velocity, and Why Does It Matter?#
Group velocity is the speed at which a group of waves (or swell) travels. This is important because it tells us how quickly wave energy moves across the ocean. In deep water, waves travel faster, but as they approach shallow water, friction with the seafloor slows them down, causing their energy to compress and the wave height to grow.
Here’s how we calculate it:
Step 1: Calculating Group Velocity in Deep Water#
In deep water, group velocity depends on the wavelength \(L\) and the wave period \(T\). Note: in this equation we will use a constant of 1.56, which is derived from the relationship between gravity and wave motion in deep water, specifically \( \frac{g}{2\pi} \), where \( g \) is the acceleration due to gravity.
Wavelength Calculation#
$$ L = 1.56 \cdot T^2 $$
Given \(T = 13 , \text{s}\):
$$ L = 1.56 \cdot 13^2 = 1.56 \cdot 169 = 263.64 , \text{m} $$
This tells us the wavelength is about 263 meters.
Group Velocity Calculation#
A factor of 0.5 is used For deep-water waves, the group velocity is always half of the phase velocity due to how energy is distributed among wave components in deep water:
$$ C_g = 0.5 \cdot \frac{L}{T} $$
Plugging in \(L = 263.64 , \text{m}\) and \(T = 13 , \text{s}\):
$$ C_g = 0.5 \cdot \frac{263.64}{13} \approx 10.14 , \text{m/s} $$
The group velocity is 10.14 meters per second, meaning the energy in the swell moves rapidly across deep water.
Step 2: Calculating Group Velocity in Shallow Water#
As waves move into shallow water, their interaction with the seabed causes the group velocity to decrease. In shallow water, group velocity is related to the depth of the water \(h\):
$$ C_{g,\text{shallow}} = \sqrt{g \cdot h} $$
Where:
- \(g = 9.8 , \text{m/s}^2\): Acceleration due to gravity,
- \(h = 3 , \text{m}\): Water depth at Main Beach.
Plugging in the values:
$$ C_{g,\text{shallow}} = \sqrt{9.8 \cdot 3} \approx 5.42 , \text{m/s} $$
As expected, the group velocity in shallow water is much slower than in deep water.
Step 3: Connecting It All—The Shoaling Factor#
Now we calculate the shoaling factor to see how much the wave height increases:
$$ K_s = \sqrt{\frac{C_g}{C_{g,\text{shallow}}}} = \sqrt{\frac{10.14}{5.42}} \approx 1.37 $$
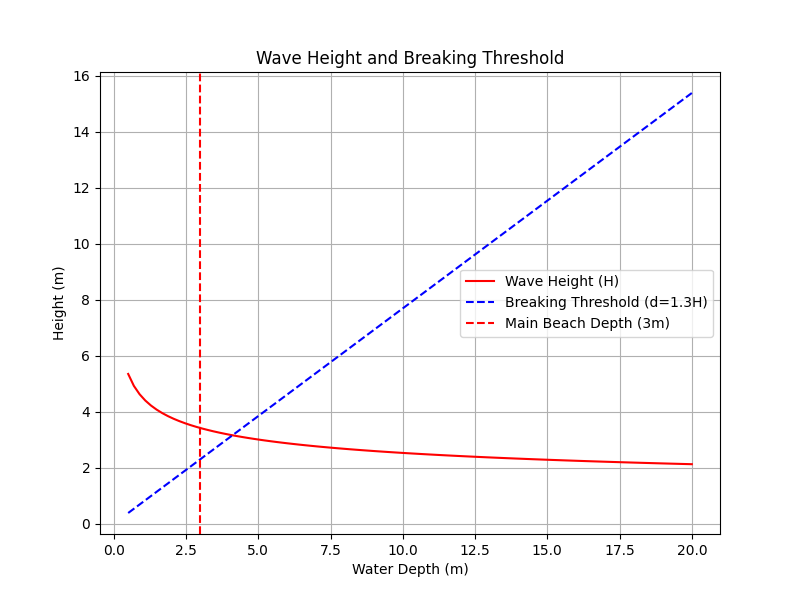
The shoaling factor of 1.37 means the wave height at Main Beach will grow by approximately 37% as the waves move from deep water to shallow water.
Step 4: Applying the Shoaling Factor to Wave Height#
To predict the wave height nearshore \(H_{\text{nearshore}}\), multiply the offshore wave height \(H_{\text{deep}}\) by the shoaling factor:
$$ H_{\text{nearshore}} = H_{\text{deep}} \cdot K_s $$
For an offshore wave height of 2.5 meters:
$$ H_{\text{nearshore}} = 2.5 \cdot 1.37 \approx 3.4 , \text{m} $$
At Main Beach, the waves will increase from 2.5 meters offshore to about 3.4 meters as they approach the shore.
Why Does This Matter?#
Understanding the shoaling factor and group velocity gives you insight into how waves behave nearshore. At Main Beach, the sandy bottom evenly distributes the wave energy, creating fun, mellow waves perfect for cruising. However, breaks with steeper bathymetry (like ridges) may focus and amplify the energy even further, creating steeper, punchier waves.
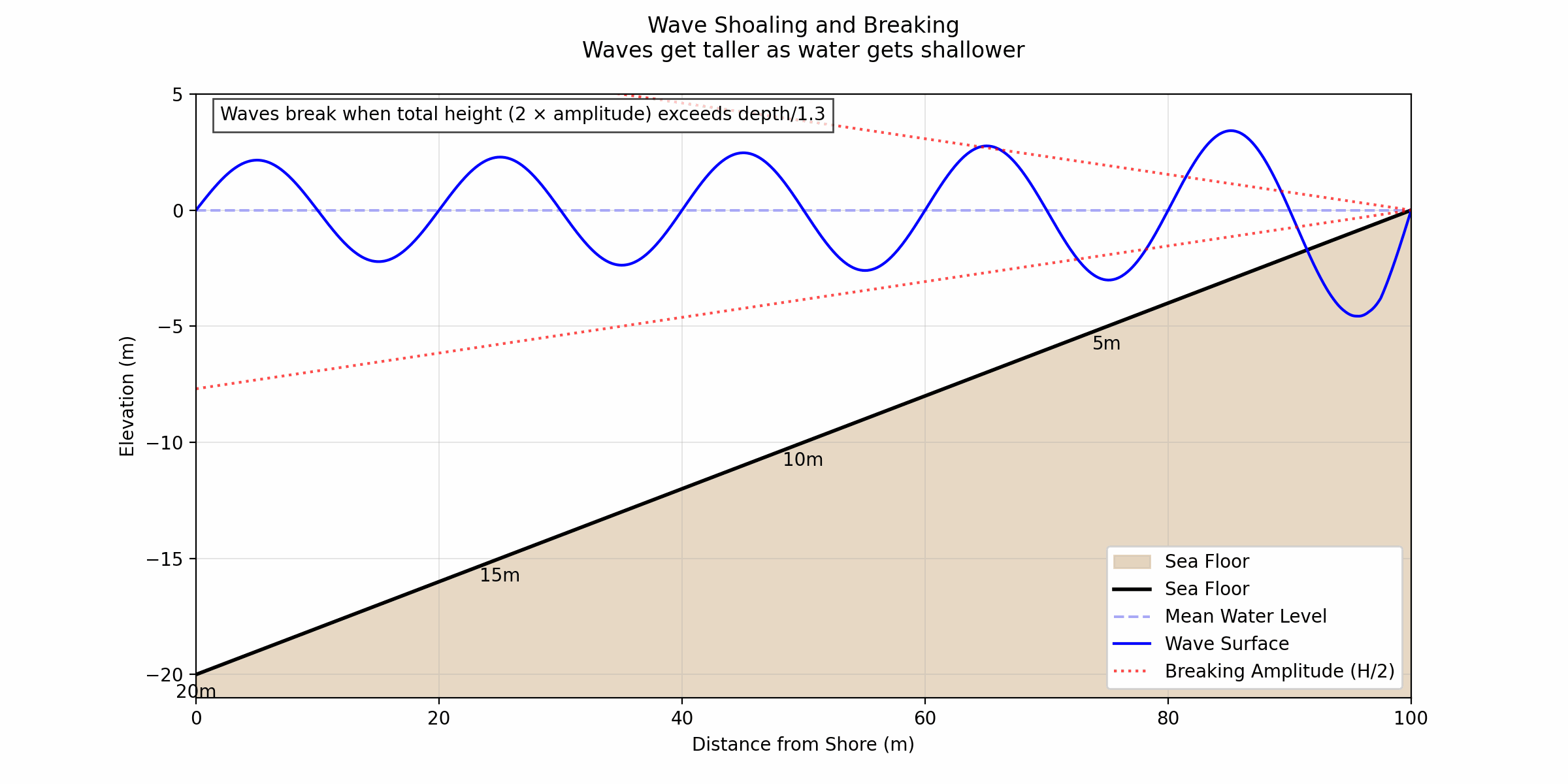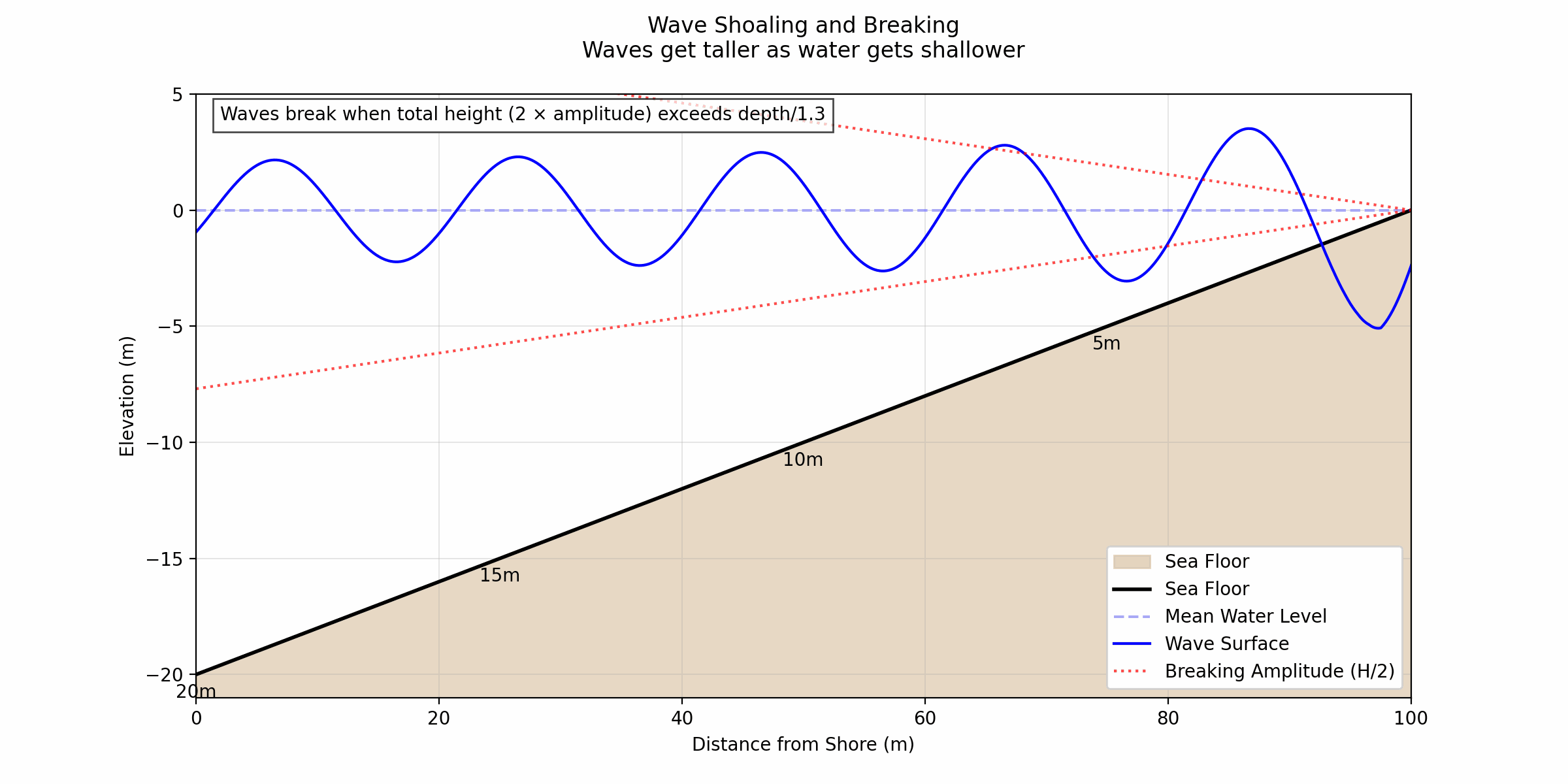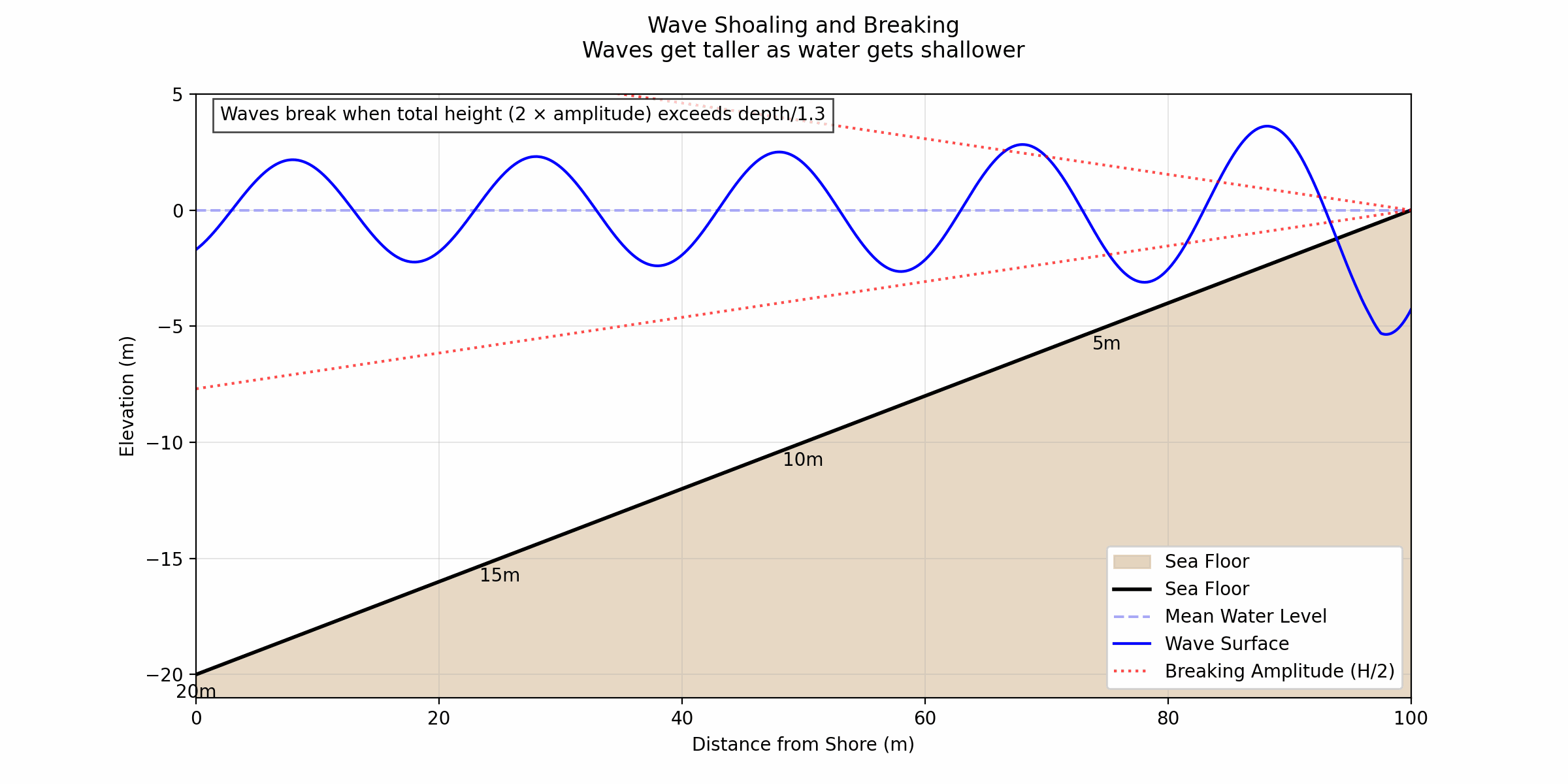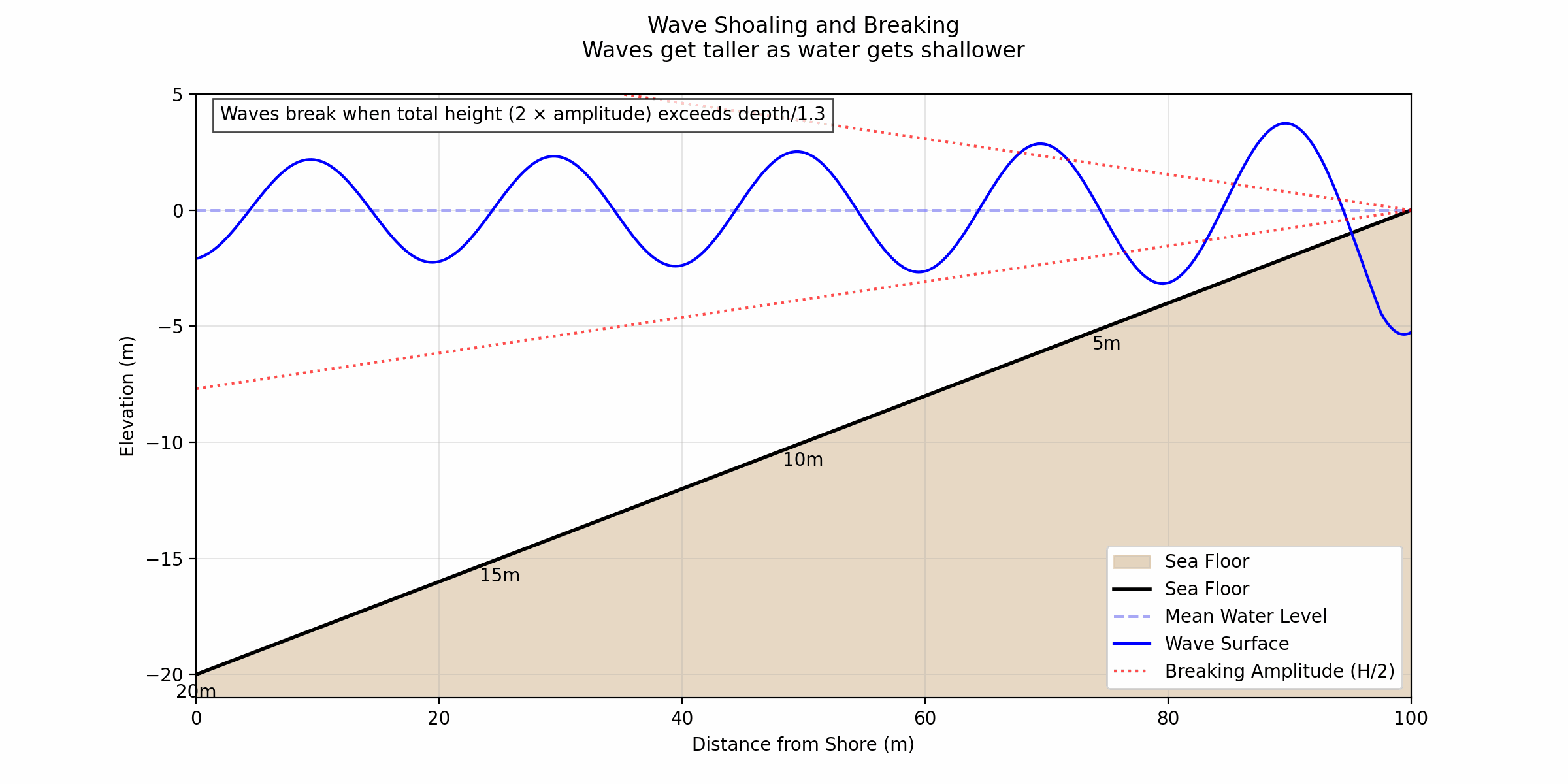
Wave Height#
If the buoy reports 2.5 m, shoaling suggests waves at Main Beach might be:
$$ H = 2.5 \cdot 1.37 \approx 3.4 , \text{m (peak-to-trough)} $$
But remember: sandy beaches don’t focus energy, so the waves will likely be softer and less steep, making them great for cruisy rides.
This concludes the first part of the series. In the next part, we will look at Secret Ridge and see how it compares to Main Beach. In this section, we will look at how unique features of the ocean floor can amplify and shape waves.